실험 기간을 좀 더 늘리면 안 돼요?
실험을 한 번 진행했는데 통계적으로 유의하지 못한 결과를 얻었습니다. 기간을 조금 더 두고 실험을 하자니 시간이 오래 걸릴 것 같은데 기존 결과를 그대로 포함해서 실험 기간을 늘려서 보면 안 되나요?
통계학도감 - 9장 회귀분석
회귀분석이란 무엇이며, 회귀분석 과정에서 사용하는 용어와 다양한 방법에 대해 알아보자.
목차
- 회귀분석: 원인과 결과의 연관을 찾는다
- 최소제곱법: 데이터에 수식을 동일하게 적용한다
- 결정계수: 회귀선의 정확도를 평가한다
- t 검정: 회귀선의 기울기를 검정한다
- 잔차분석: 분석의 적절성을 검토한다
- 중회귀분석: 원인이 여럿일 때의 회귀분석
- 다중공선성: 설명변수 간의 문제
- 변수선택법: 유효한 설명변수를 고른다
- 절편 더미: 질의 차이를 설명하는 변수
- 기울기 더미: 질의 차이를 설명하는 변수
- 프로빗 분석: 더미변수를 이용한 회귀분석
!pip install --upgrade -q gspread
회귀분석
회귀분석은 변수 x(원인)가 변수 y(결과)에 주는 영향을 알기 위한 방법이다. 변수 x와 변수 y 사이에 있는 관계를 직선 또는 곡선의 식으로 나타낸 것을 회귀선이라고 한다.
회귀선
- 회귀분석을 이용하면 원인이 결과에 주는 영향의 정도를 수치화할 수 있고 예측 등에 이용할 수 있다.
- 추정된 관계(회귀선)가 통계적으로 의미있는 것인지 아닌지를 확인할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 만들기
marketing = np.random.randint(5, 40, 100)
sales = marketing * 2 + np.random.randint(-10, 10, 100)
# 산점도 그리기
plt.scatter(x = marketing, y = sales)
plt.xlabel('Marketing Spending')
plt.ylabel('Sales')
plt.axis([0, 40, 0, 100])
plt.show()
print('Correlation \n', np.corrcoef(marketing, sales))
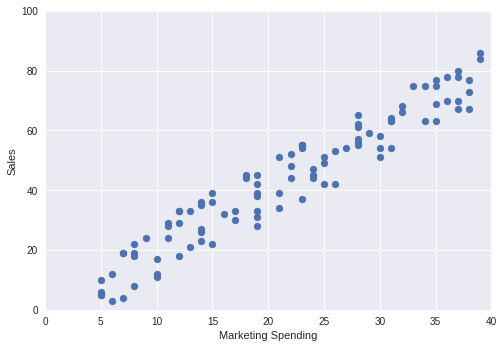
Correlation
[[1. 0.96068706]
[0.96068706 1. ]]
# sci-kit learn 라이브러리에서 linear_model 모듈 불러오기
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
lm = linear_model.LinearRegression()
model = lm.fit(marketing.reshape(-1, 1), sales)
sales_pred = model.predict(marketing.reshape(-1, 1))
print('Coefficients: \n', model.coef_) # 계수 확인하기
print('Mean squared error: %.2f'
% mean_squared_error(sales, sales_pred)) # RMSE 확인하기
print('Variance score: %.2f' % r2_score(sales, sales_pred)) # R-squared 확인하기
plt.scatter(marketing, sales, color = 'black')
plt.plot(marketing, sales_pred, color = 'blue', linewidth = 3)
plt.xlabel('Marketing Spending')
plt.ylabel('Sales')
plt.axis([0, 40, 0, 100])
plt.show()
Coefficients:
[2.02931856]
Mean squared error: 34.72
Variance score: 0.92
회귀식의 이론 모델
\[y = \beta_0 + \beta_1 x + \epsilon\]- $y$ : 피설명변수, 종속변수
- $\beta_0$ : 절편
- $\beta_1$ : 기울기
- $\epsilon$ : 오차항, ~ N(0, 1)
최소제곱법을 이용해서 추정한 회귀식
\[\hat{y} = \hat{\beta_0} + \hat{\beta_1} x\]- $\hat{y} $ : $y$ 의 예측값
- $\hat{\beta_0}$ : $\beta_0$ 의 추정치
- $\hat{\beta_1}$ : $\beta_1$ 의 추정치
파라미터와 추정값
- 파라미터는 수치가 들어가는 것은 알고 있지만 아직 어떤값이 될지 모른다는 것을 나타낸다.
- 추정값은 구체적인 수치를 알고 있는 것으로 취급한다. (불편추정량과 기호는 같지만 의미는 다르다.)
2. 최소제곱법 (OLS; Ordinary Least Squares)
- 최소제곱법은 회귀선의 파라미터 값을 추정하는 방법 중 하나이다.
- 잔차($\hat{\epsilon}$) 란 관측값과 예측값의 차이($y - \hat{y}$) 을 말한다.
- 관측데이터($x_i, y_i$) 에 잘 들어맞는 직선을 긋고 싶다.
- 회귀선과 관측 데이터까지의 잔차를 최소로 한다.
- 잔차를 제곱해서 더하고 (잔차제곱합, SSR) 그것이 최소가 되도록 절편과 기울기를 선택한다.
- 회귀선이 추정된다.
SST = SSR + SSE
- SST(Total Sum of Squared) : $\sum_i^n{(y_i - \bar{y})^2}$
- SSR(Residual Sum of Squared) : $\sum_1^n{\epsilon_i^2} = \sum_i^n{(\hat{y}_i - \bar{y})^2}$
- SSE(Error Sum of Squared) : $\sum_i^n (y_i - \hat{y_i})^2$
최소제곱법으로 추정값 구하는 법(단순회귀의 경우)
- 함수 J는 x와 y 의 함수가 아니라 $\hat{\beta_0}$ 와 $\hat{\beta_1}$ 의 함수로 생각한다.
- 둘 이상의 변수가 있는 함수를 하나의 함수에 대해 미분하는 것을 편미분이라고 한다.
- 편미분의 기호는 ‘$d$’ 가 아니라 ‘$\partial$’을 이용한다.
- 하나의 변수에 대해 편미분할 때 그 이외의 변수는 상수로 취급한다.
- 그런데 함수 J 를 $\hat{\beta_0}$ 와 $\hat{\beta_1}$에 대해 각각 편미분하면 다음과 같다.
- $\frac{\partial J}{\partial \hat{\beta_0}} = \sum \frac{\partial}{\partial \beta_0} (y_i - \beta_0 - \beta_1 x_i)^2$
3. 결정계수: 회귀선의 정확도를 평가한다
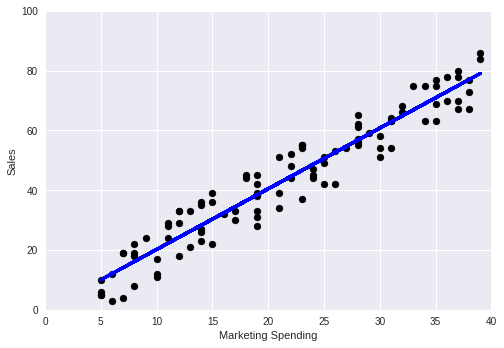
결정계수는 추정된 회귀선이 얼마나 관측 데이터에 들어맞을지(어느 정도의 적합성을 갖고 있을지)를 가늠하는 지표이다. 0에서 1 사이의 값을 취하며, 1에 가까울수록 전체 변동에서 추정된 회귀선으로 설명할 수 있는 변동이 높다는 말이다.
단순선형회귀에서의 결정계수는 관측값($y$)과 예측값($\hat{y}$)의 상관계수의 제곱과 같다.
\[R^2 = \frac{예측값으로 설명되는 변동}{전체 변동} = \frac{\sum(\hat{y_i} - \bar{y})^2}{\sum(y_i - \bar{y})^2}\]
# 결정계수
model.score(marketing.reshape(-1, 1), sales)
0.9229196312391211
4. t 검정: 추정된 회귀선의 기울기를 검정한다
추정된 회귀계수가 0과 같은 경우, 변수 x는 변수 y 의 원인이라고 할 수 없다. 이를 통계적으로 확인하기 위해 $H_0 : \beta_1 = 0\ vs\ H_1: \beta_1 \ne 0$ 으로 해서 가설검정을 한다.
- 표본평균이 확률변수이듯이 표본으로부터 추정하는 회귀계수(절편과 기울기)도 확률변수이다. 즉, 서로 다른 표본에서 추정되는 회귀 계수의 값이 다를 수 있다.
- 추정된 기울기가 0과 통계적으로 다른지 어떤지는 회귀분석에서 중요한 의미를 갖는다.
t 검정
- $\hat{\beta_1}$ 은 평균이 $\beta_1$이고 분산이 $\frac{\sigma^2}{\sum({x_i - \bar{x}})^2}$ 인 정규분포를 따른다. 여기서 $\sigma^2$ 은 오차항의 분산을 나타낸다.
- 그러나 오차항의 분산($\sigma^2$) 을 아직 모르므로 잔차($\hat{e_i}^2$) 를 사용해 표본에서 추정한다($\sigma^2 => \hat{\sigma^2} = \frac{\sum\hat{e_i}^2}{n - 2}$). 여기서 $n - 2$ 는 $\sum\hat{e_i}^2$ 의 자유도이다.
- $\hat{\sigma}^2$ 을 이용해서 $\hat{\beta_1}$ 의 준표준화변량(t값)을 구하면 $t = \frac{\hat{\beta_1} - \beta_1}{\sqrt{\hat{\sigma}^2 / \sum(x_i - \bar{x})^2}}$ 이 된다. 이것은 자유도 $n 2 $ 인 t 분포를 따른다.
- 가설 설정
- $H_0 : \beta_1 = 0$
- $H_1: \beta_1 \ne 0$
- $t = \frac{\hat{\beta_1} - \beta_1}{\sqrt{\hat{\sigma}^2 / \sum(x_i - \bar{x})^2}}$ 에 $\beta_1 = 0$ (귀무가설)을 대입
- $t값 =\frac{회귀계수의 추정값}{\hat{\beta_1} 의 불편표준오차} = \frac{\hat{\beta_1}}{\sqrt{\hat{\sigma}^2 / \sum(x_i - \bar{x})^2}}$
- $|t| > t_{n-2, \alpha/2}$ 일 때, $H_0$ 를 기각($t_{n-2, \alpha/2}$ 는 자유도 $n-2$ 일 때 유의수준 $\alpha/2$ 의 t값)
5. 잔차분석: 분석의 적절성을 검토한다.
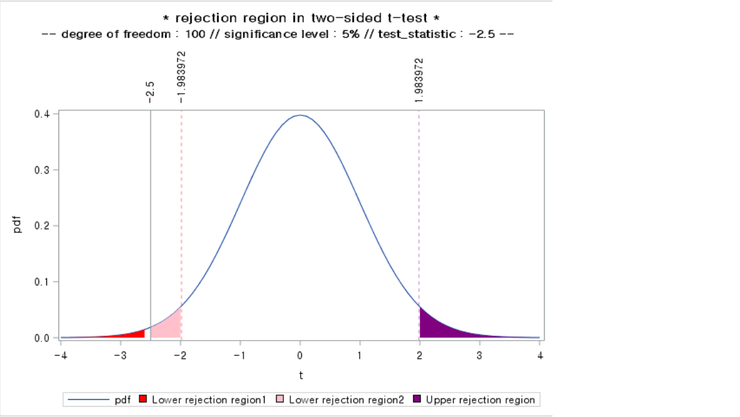
잔차($\hat{\epsilon}$) 와 예측값($\hat{y}$) 의 산포도(잔차 플롯)를 그리면 데이터의 문제(이상치가 포함되어 있음)나 모델의 문제(회귀식이 부적절)을 발견할 수 있다.
단순선형회귀분석에서 잔차 플롯은 아래의 항목들을 만족해야 한다.
- 잔차는 정규분포를 따른다(정규성).
- 잔차의 분산은 일정하다(등분산성).
- 잔차는 서로 독립이다(독립성).
- 잔차에는 특정한 패턴이 보이지 않아야한다.
- 이상치가 없어야한다.
import seaborn as sns
resid = sales - sales_pred
sns.residplot(sales_pred, resid, lowess = True, color = 'g')
6. 다중회귀분석: 원인이 여럿일 때의 회귀분석
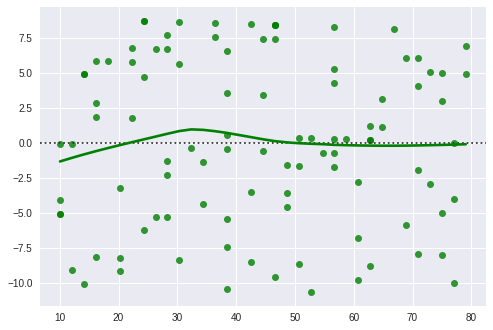
설명변수가 여러 개 있을 경우는 다중회귀분석을 이용한다. 설명변수의 수가 다른 회귀식의 적합도를 비교할 경우에는 자유도 조정이 끝난 결정계수(Adjusted $R^2$)를 이용한다.
편회귀계수
- 다중회귀분석의 회귀계수를 편회귀계수라고 한다.
- 편회귀계수는 회귀식에 포함되는 다른 변수의 영향을 제거한 후의 (다른 변수를 ‘일정’으로 했을 때의), 해당 설명변수가 반응변수에 주는 영향을 나타낸다.
- 설명변수가 두 개인 경우 회귀선이 아니라 회귀평면으로 추정한다.
표준편회귀계수
- 모든 변수(설명변수, 반응변수)를 표준화해서 중회귀분석을 했을 때의 회귀계수이다.
- 단위가 다른 설명변수 간에 회귀계수의 크기를 비교할 경우에 사용한다.
- 표준화된 반응변수의 평균값은 0이기 때문에 절편 $\beta_0$ 도 0이다.
자유도가 조정된 결정계수(Adjusted $R^2$)
- 결정계수는 설명변수를 늘리면 값이 커지는 결점이 있다.
- 그래서 변수를 추가해도 결정계수의 값이 증가하지 않도록 고안한 지표가 자유도 조정 결정계수(Adjusted $R^2$) 이다.
- 설명변수의 수가 다른 여러 회귀식(반응변수는 같음)의 적합도를 비교할 때 사용한다.
- 자유도가 조정된 결정계수는 거의 통계분석용 소프트웨어에서 출력되지만, 결정계수로도 간단히 구할 수 있다.
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 데이터 불러오기
dat = sm.datasets.get_rdataset('Guerry', 'HistData').data
# 데이터 확인하기
print(dat.describe())
# 회귀식 적합하기
model1 = smf.ols('Lottery ~ Literacy + np.log(Pop1831)', data = dat).fit()
model2 = smf.ols('Lottery ~ Literacy + np.log(Pop1831) + np.log(Crime_prop)', data = dat).fit()
# 결과 확인하기
print(model1.summary())
print(model2.summary())
dept Crime_pers Crime_prop Literacy Donations \
count 86.000000 86.000000 86.000000 86.000000 86.000000
mean 46.883721 19754.406977 7843.058140 39.255814 7075.546512
std 30.426157 7504.703073 3051.352839 17.364051 5834.595216
min 1.000000 2199.000000 1368.000000 12.000000 1246.000000
25% 24.250000 14156.250000 5933.000000 25.000000 3446.750000
50% 45.500000 18748.500000 7595.000000 38.000000 5020.000000
75% 66.750000 25937.500000 9182.250000 51.750000 9446.750000
max 200.000000 37014.000000 20235.000000 74.000000 37015.000000
Infants Suicides Wealth Commerce Clergy \
count 86.000000 86.000000 86.000000 86.000000 86.000000
mean 19049.906977 36522.604651 43.500000 42.802326 43.430233
std 8820.233546 31312.532649 24.969982 25.028370 24.999549
min 2660.000000 3460.000000 1.000000 1.000000 1.000000
25% 14299.750000 15463.000000 22.250000 21.250000 22.250000
50% 17141.500000 26743.500000 43.500000 42.500000 43.500000
75% 22682.250000 44057.500000 64.750000 63.750000 64.750000
max 62486.000000 163241.000000 86.000000 86.000000 86.000000
Crime_parents Infanticide Donation_clergy Lottery Desertion \
count 86.000000 86.000000 86.000000 86.000000 86.000000
mean 43.500000 43.511628 43.500000 43.500000 43.500000
std 24.969982 24.948297 24.969982 24.969982 24.969982
min 1.000000 1.000000 1.000000 1.000000 1.000000
25% 22.250000 22.250000 22.250000 22.250000 22.250000
50% 43.500000 43.500000 43.500000 43.500000 43.500000
75% 64.750000 64.750000 64.750000 64.750000 64.750000
max 86.000000 86.000000 86.000000 86.000000 86.000000
Instruction Prostitutes Distance Area Pop1831
count 86.000000 86.000000 86.000000 86.000000 86.000000
mean 43.127907 141.872093 207.953140 6146.988372 378.628721
std 24.799809 520.969318 109.320837 1398.246620 148.777230
min 1.000000 0.000000 0.000000 762.000000 129.100000
25% 23.250000 6.000000 121.383000 5400.750000 283.005000
50% 41.500000 33.000000 200.616000 6070.500000 346.165000
75% 64.750000 113.750000 289.670500 6816.500000 444.407500
max 86.000000 4744.000000 539.213000 10000.000000 989.940000
OLS Regression Results
==============================================================================
Dep. Variable: Lottery R-squared: 0.348
Model: OLS Adj. R-squared: 0.333
Method: Least Squares F-statistic: 22.20
Date: Sun, 09 Dec 2018 Prob (F-statistic): 1.90e-08
Time: 13:13:44 Log-Likelihood: -379.82
No. Observations: 86 AIC: 765.6
Df Residuals: 83 BIC: 773.0
Df Model: 2
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 246.4341 35.233 6.995 0.000 176.358 316.510
Literacy -0.4889 0.128 -3.832 0.000 -0.743 -0.235
np.log(Pop1831) -31.3114 5.977 -5.239 0.000 -43.199 -19.424
==============================================================================
Omnibus: 3.713 Durbin-Watson: 2.019
Prob(Omnibus): 0.156 Jarque-Bera (JB): 3.394
Skew: -0.487 Prob(JB): 0.183
Kurtosis: 3.003 Cond. No. 702.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
OLS Regression Results
==============================================================================
Dep. Variable: Lottery R-squared: 0.403
Model: OLS Adj. R-squared: 0.381
Method: Least Squares F-statistic: 18.44
Date: Sun, 09 Dec 2018 Prob (F-statistic): 3.11e-09
Time: 13:13:44 Log-Likelihood: -376.08
No. Observations: 86 AIC: 760.2
Df Residuals: 82 BIC: 770.0
Df Model: 3
Covariance Type: nonrobust
======================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept 65.9147 74.285 0.887 0.377 -81.861 213.690
Literacy -0.3415 0.134 -2.544 0.013 -0.608 -0.074
np.log(Pop1831) -26.7902 5.990 -4.472 0.000 -38.706 -14.874
np.log(Crime_prop) 16.6622 6.099 2.732 0.008 4.529 28.796
==============================================================================
Omnibus: 2.539 Durbin-Watson: 2.052
Prob(Omnibus): 0.281 Jarque-Bera (JB): 2.431
Skew: -0.404 Prob(JB): 0.297
Kurtosis: 2.841 Cond. No. 1.55e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.55e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
7. 다중공선성: 설명변수 간의 문제
- 설명변수들 간에 높은 상관관계(다중공선성)가 있을 경우, 회귀계수가 기대한 부호(+, -)가 되지 않는 등 결과를 해석하기 어려워질 수가 있다.
- 다중공선성을 발견하려면 VIF(Variance Inflation Factor; 분산팽창요인)와 허용도라는 지표를 이용한다.
설명변수 간의 관련
- 설명변수 간에 강한 관련성이 있을 때, 다중공선성이 있다고 한다.
- 특히 변수 $x_1$과 변수 $x_2$ 사이에 완전한 상관관계(상관계수 = 1)가 있을 때, 완전 다중공선성이 생겼다고 한다. 이 경우에는 추정이 불가능하다(어느 한쪽의 변수를 회귀식에서 제거해야 한다).
- 여러 설명변수들 사이에서 한 설명변수를 다른 설명변수들의 함수로 나타낼 수 있는 경우에도 마찬가지이다.
- (불완전한) 다중공선성의 경우에는 추정값을 구할 수가 있다. 그러나 어떤 변수의 변동이 다른 변수의 변동에 강하게 영향을 미치기 때문에 편회귀계수의 표준오차가 커져 추정값의 신뢰도가 낮아진다.
VIF(분산팽창요인)
- 다중공선성을 발견하기 위한 지표로, 회귀계수의 분산(표준오차)이 얼마나 커지는지를 나타낸다.
- $R_i^2$: $i$번째 설명변수를 반응변수로 두고 나머지 설명변수로 회귀분석을 진행했을 때의 결정계수
- 대부분의 통계 소프트웨어에서는 VIF 를 출력하므로 이 값이 10이 넘지 않는지 체크한다.
- VIF 가 10보다 클 경우 변수를 제외하거나 합성하는 등의 대응이 필요하다.
- 허용도(tolerance)를 이용할 경우에는 0.1 이상이면 문제가 없다고 할 수 있다.
8. 변수선택법: 유효한 설명변수를 고른다
- 어느 설명변수를 회귀식에 포함시킬지를 정하는 방법이다.
- 대부분의 통계 소프트웨어는 자동적으로 변수를 선택하도록 할 수 있다.
- 회귀식에서 변수를 삭제하는 기준, 회귀식에 변수를 t 검정의 p값(=0.1) 외에 t 값을 제곱한 F 값(=2.0) 을 많이 사용한다.
- 일반적으로는 AIC(Akaike Information Criterion) 을 주로 사용하고, 그 외에도 BIC(Bayes Information Criterion), Likelihood Ratio Test 를 사용하기도 한다.
변수 선택 방법
- 전진선택법 (Forward Selection):설명변수가 0개인 모형부터 시작해서 변수를 하나씩 추가하는 방법
- 후진제거법 (Backword Elimination): 모든 설명변수를 넣은 모형부터 시작해서 변수를 하나씩 제거하는 방법
- 단계선택법(Step-wise Selection): 모든 설명변수를 넣은 모형부터 시작해서 단계마다 변수를 제거 및 추가하는 방법
- 모든 부분집합 회귀(All subset regression): Stepwise regression 에서는 모든 가능한 모형을 비교해주지는 않기 때문에 여기서 선택된 모형이 최선의 모형이라는 보장이 없다. 그래서 모든 가능한 조합을 보여주는 변수 선택 방법을 사용하기도 한다.
9. 절편 더미: 질의 차이를 설명하는 변수 (1)
- 더미 변수(dummy variable)란 1 또는 0의 값을 취하는 변수를 의미한다.
- 더미변수를 이용하면 집단간의 차이를 검정할 수 있다.
절편 더미를 이용한 회귀식
\[y = \beta_0 + \beta_1x + \beta_2D + \epsilon\]- 계수 $\beta_2$ 가 통계적으로 유의할 때 회귀선의 절편이 집단마다 다르다.
from sklearn.datasets import load_boston
import pandas as pd
import statsmodels.api as sm
boston = load_boston()
boston_features = pd.DataFrame(boston.data, columns = boston.feature_names)
dummy_chas = pd.get_dummies(boston_features.CHAS)
boston_features = boston_features.join(dummy_chas)
boston_features = sm.add_constant(boston_features)
boston_features = boston_features.drop('CHAS', axis = 1)
boston_target = pd.DataFrame(boston.target, columns = ['MEDV'])
model = sm.OLS(boston_target, boston_features)
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.741
Model: OLS Adj. R-squared: 0.734
Method: Least Squares F-statistic: 108.1
Date: Mon, 10 Dec 2018 Prob (F-statistic): 6.95e-135
Time: 15:49:27 Log-Likelihood: -1498.8
No. Observations: 506 AIC: 3026.
Df Residuals: 492 BIC: 3085.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 25.2236 3.407 7.403 0.000 18.529 31.918
CRIM -0.1072 0.033 -3.276 0.001 -0.171 -0.043
ZN 0.0464 0.014 3.380 0.001 0.019 0.073
INDUS 0.0209 0.061 0.339 0.735 -0.100 0.142
NOX -17.7958 3.821 -4.658 0.000 -25.302 -10.289
RM 3.8048 0.418 9.102 0.000 2.983 4.626
AGE 0.0008 0.013 0.057 0.955 -0.025 0.027
DIS -1.4758 0.199 -7.398 0.000 -1.868 -1.084
RAD 0.3057 0.066 4.608 0.000 0.175 0.436
TAX -0.0123 0.004 -3.278 0.001 -0.020 -0.005
PTRATIO -0.9535 0.131 -7.287 0.000 -1.211 -0.696
B 0.0094 0.003 3.500 0.001 0.004 0.015
LSTAT -0.5255 0.051 -10.366 0.000 -0.625 -0.426
0.0 11.2675 1.733 6.501 0.000 7.862 14.673
1.0 13.9561 1.781 7.836 0.000 10.457 17.455
==============================================================================
Omnibus: 178.029 Durbin-Watson: 1.078
Prob(Omnibus): 0.000 Jarque-Bera (JB): 782.015
Skew: 1.521 Prob(JB): 1.54e-170
Kurtosis: 8.276 Cond. No. 1.23e+18
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 1.05e-28. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
10. 기울기 더미: 질의 차이를 설명하는 변수 (2)
- 절편과 기울기에도 그룹 간에 차이를 나타내는 경우가 있다. 그 경우에는 기울기(계수) 더미를 사용한다. 기울기 더미는 더미 변수와 설명 변수를 곱해서 만든다.
- 계수 $\beta_3$ 가 통계적으로 유의할 때 회귀선의 기울기 가 그룹마다 다르다.
- 절편에 차이가 없을 때는 기울기 더미만으로도 충분하다.
11. 프로빗 분석: 더미변수를 이용한 회귀분석
- 반응변수가 더미변수인 경우에 이용하는 분석방법이다.
선택 확률
- 아래 그림은 자동차 구매(z = 1: 구입했다, z = 0: 구입하지 않았다)와 구입자의 소득관계를 그래프로 나타낸 것이다.
- 반응변수가 더미변수라도 최소제곱법(OLS)에 의해 회귀선을 얻을 수 있다. 하지만 예측값이 0과 1의 범위 밖에 있을 수도 있고, 오차항의 분산도 일정하지 않으므로 OLS 를 이용한 분석은 바람직하지 않다.
2025
A/B 테스트가 통계학을 망치고 있다
A/B 테스트란 무엇이고, 제가 왜 이게 통계학을 망치고 있다고 생각하는지 설명드리고자 합니다.
(번역) AI 가 우리에게 다가오고 있다
이 글은 AI가 데이터베이스에 직접 접근해 인간 전문가처럼 데이터를 분석하는 새로운 워크플로우를 소개합니다. 단순한 질의응답을 뛰어넘는 이러한 도약은 데이터 분석가의 역할이 근본적으로 재정의될 미래를 암시합니다.
(번역) 넷플릭스 게임 사용자의 모험
이 글은 넷플릭스 (Netflix) 에서의 분석 엔지니어링 (Analytics Engineering) 관련 업무의 범위를 공유하기 위한 여러 편의 글 중 두 번째 글이며, 최근에 열렸던 분석 엔지니어링 컨퍼런스에서 발표된 내용이기도 합니다. 더 많은 내용이 궁금하신가요? 첫 번째 ...
(번역) 듀오링고가 사용자의 성장에 다시금 불을 지핀 방법 - Part 3
듀오링고의 350% 성장의 뒷 이야기, 리더보드, 연속 학습, 알림, 그리고 혁신적인 그로스 모델 들어가기에 앞서
(번역) 듀오링고가 사용자의 성장에 다시금 불을 지핀 방법 - Part 2
듀오링고의 350% 성장의 뒷 이야기, 리더보드, 연속 학습, 알림, 그리고 혁신적인 그로스 모델 들어가기에 앞서
(번역) 듀오링고가 사용자의 성장에 다시금 불을 지핀 방법 - Part 1
듀오링고의 350% 성장의 뒷 이야기, 리더보드, 연속 학습, 알림, 그리고 혁신적인 그로스 모델
(번역) 의미있는 지표 (데이터로 제품팀이 집중해야할 것을 뾰족하게 만든 방법)
원문: Meaningful metrics: How data sharpened the focus of product teams
2023
(번역) Booking.com 에서의 축차 검정 (Sequential Testing)
원문: Sequential Testing at Booking.com
영어랑 친해지는 방법
가장 좋은 방법은 당연히 영어 밖에 사용하지 못하는 환경에 강제로 처해지는 것이겠지만 그것이 어려우니…
신입 데이터 분석가를 꿈꾸는 분들에게
고민의 흔적을 보여주세요
데이터 트래킹 기깔나게 잘 하는 방법
을 찾습니다.
2022
(번역) 차트와 접근성
원문: Charts & Accessibility
2020
모수, 큰 수의 법칙, 그리고 중심극한정리
모수, 큰 수의 법칙, 그리고 중심극한정리에 대하여
(번역) 내가 COVID-19 데이터를 시각화하지 않는 이유
그리고 여러분들도 (아마도) 하지 않아야 하는 이유
사내 스터디에 대한 회고
회사 서비스의 추천 시스템을 개선하기 위해 팀 내에서 (아직까진 두 명이긴 하지만) 지난 두 달 동안 스터디를 진행했습니다. 얼마 전 두 번째 스터디가 끝났고 이에 대한 회고를 해보려고 합니다.
(번역) 데이터의 어두운 면 - 개인정보 (Dark Side of Data:Privacy)
원문: Dark Side of Data: Privacy by Emre Rencberoglu
(번역) 초보자를 위한 RStudio 의 프로젝트 와 작업 디렉토리
원문: RStudio Projects and Working Directories: A Beginner’s Guide by Martin Chan
(번역) Tidy Tuesday 이벤트에 대한 소개
원문: TidyTuesday GitHub Repository
(번역) 프로그래밍 언어들의 이름을 지은 방법
원문: How programming languages got their names
2019
(번역) 회의를 덜 끔찍하게 만드는 방법
원문: How to Make Meetings Less Terrible 팟캐스트: How to Make Meetings Less Terrible (Ep. 389)
R 에서 networkD3 를 이용해서 샌키 다이어그램(Sankey Diagram) 그리기
생키 다이어그램 (Sankey Diagram) 은 흐름(Flow) 다이어그램의 한 종류로써 그 화살표의 너비로 흐름의 양을 비율적으로 보여준다.
(번역) 2016년 모든 데이터 사이언티스트가 알아야할 10+2 가지 데이터 사이언스 방법론
2년 전 일본어로 책을 내긴 했지만 대부분의 독자들이 이 책을 읽을 수는 없을 것 같았다.
(번역) 29가지 통계 개념 - 자기회귀 모형의 정의와 자기회귀 과정(AR Process)
자기회귀 모형이란 무엇인가?
(번역) 29가지 통계 개념 - 회귀분석의 가정과 조건들
회귀분석을 실행하기 위해 필요한 가정과 조건들에 대해 알아보자.
(번역) 29가지 통계 개념 - 정규성 가정
통계적 검정과 회귀분석에서 자주 사용되는 정규성 가정과 정규성 검정에 대해 알아보자.
(번역) 29가지 통계 개념 - 독립성 가정
여러 통계 검정과 모형에서 사용되는 독립성 가정에 대해 알아보자.
(번역) 29가지 통계 개념 - ARMA 모형
시계열 모형 중 ARMA 모형에대해 알아보자.
(번역) 29가지 통계 개념 - 통계학에서의 넓이에 대한 원칙
시각화에서 주의할 점인 넓이를 표시하는 원칙에 대해 알아보자.
(번역) 29가지 통계 개념 - 평균으로부터 양쪽으로 떨어진 z-값 사이의 넓이
평균 양쪽의 z-값들 사이의 넓이를 구하는 방법에 대해 알아보자.
(번역) 29가지 통계 개념 - 분산분석(Analysis of Variance)
분산분석의 개념과 방법에 대해 알아보자.
(번역) 29가지 통계 개념 - 공분산분석(Analysis of Covariance)
분산분석(ANOVA; ANalysis Of VAriance) 와 회귀분석의 개념을 섞은 공분산분석(ANCOVA; ANalysis of COVAriance)에 대해 알아보자. 이 글을 이해하기 위해서는 아래의 글을 먼저 읽는 것이 좋다.
(번역) 29가지 통계 개념 - Akaike’s Information Criterion(AIC)의 정의와 공식
Akaike’s Information Criterion 의 정의와 이를 구하는 방법에 대해 알아보자.
(번역) 29가지 통계 개념 - 수정된 R제곱 무엇에 사용하는 것인가?
수정된 R제곱과 그 용도에 대해서 알아보자.
(번역) 29가지 통계 개념- 정확도와 정밀도(Accuracy and Precision)
통계 용어 중 정확도(Accuracy)와 정밀도(Precision) 에 대해서 알아보자.
(번역) 29가지 통계 개념 - 절대 오차와 평균 절대 오차(MAE)
절대 오차와 평균 절대 오차에 대해서 알아보자.
통계학도감 - 5장 가설 검정
가설 검정이란 무엇이며, 가설 검정의 다양한 방법에 대해 알아보자.
통계학도감 - 9장 회귀분석
회귀분석이란 무엇이며, 회귀분석 과정에서 사용하는 용어와 다양한 방법에 대해 알아보자.
GitHub Pages Jekyll Blog 에 MathJax 추가하기
이 글은 MathJax 를 GitHub Pages Jekyll blog 에 추가하는 방법을 다룬다. 이탤릭체로 된 부분은 본문에는 없고 제가 따라하면서 고치거나 추가한 부분이니 참고하세요.
(번역) 29가지 통계 개념 - 통계학에서의 10% 조건이란 무엇인가?
모집단과 표본집단을 이용하는 경우 통계학에서 말하는 10% 조건이 무엇인지에 대해 알아보자.
GitHub 블로그에 Jupyter notebook 올리는 방법
여러분의 GitHub 블로그에 Jupyter notebook 을 바꿔서 올릴 수 있도록 도와줄 글입니다. 직접 바꾸는 방법은 1회성 글들을 위해서 추가했고, 변환 과정과 파일 이동, 그리고 여러분의 블로그에 올리는 것까지 한 번에 할 수 있는 자동화 bash 를 만드는 자세한 방법...
(번역) 29가지 통계 개념 - 통계학에서의 68, 95, 99.7의 법칙(68 95 99.7 Rule in Statistics)
68 95 99.7의 법칙이란 무엇인가?
(번역) 29가지 통계 개념 - ADF(Augmented Dicky Fuller) 검정
단위근 검정 방법 중 하나인 Augmented Dickey Fuller 검정에 대해 알아보자.
(번역) 쉽게 풀어 쓴 29가지 통계 개념(29 Statistical Concepts Explained in Simple English)
이 자료는 데이터 과학과 관련된 특정 주제에 대한 연재물이며, 다룰 주제는 다음과 같다. 회귀분석, 군집화, 신경망, 딥러닝, 의사결정나무, 앙상블, 상관관계, 파이썬, R, 텐서플로우, SVM, 데이터 축소, 피쳐 선택, 실험 계획법, 교차검증, 모델 피팅 등. 이 글을 계속 받...