29가지 통계 개념 - 평균으로부터 양쪽으로 떨어진 z-값 사이의 넓이

평균 양쪽의 z-값들 사이의 넓이를 구하는 방법에 대해 알아보자.

평균 양쪽의 z-값들 사이의 넓이를 구하는 방법

z-값들 사이의 넓이를 구하고자 한다면, 그 두 z-값들이 평균의 한쪽에 있는지, 또는 양쪽에 있는지에 따라 구하는 방법이 다르다. 이 글에서는 z-값들이 평균의 양쪽에 있는 경우에 그 넓이를 구하는 방법에 대해서만 살펴볼 것이다. 한쪽에 있는 경우에 대해서는 평균의 한쪽에 있는 z-값 사이의 넓이를 구하는 방법을 참고하길 바란다.

1단계

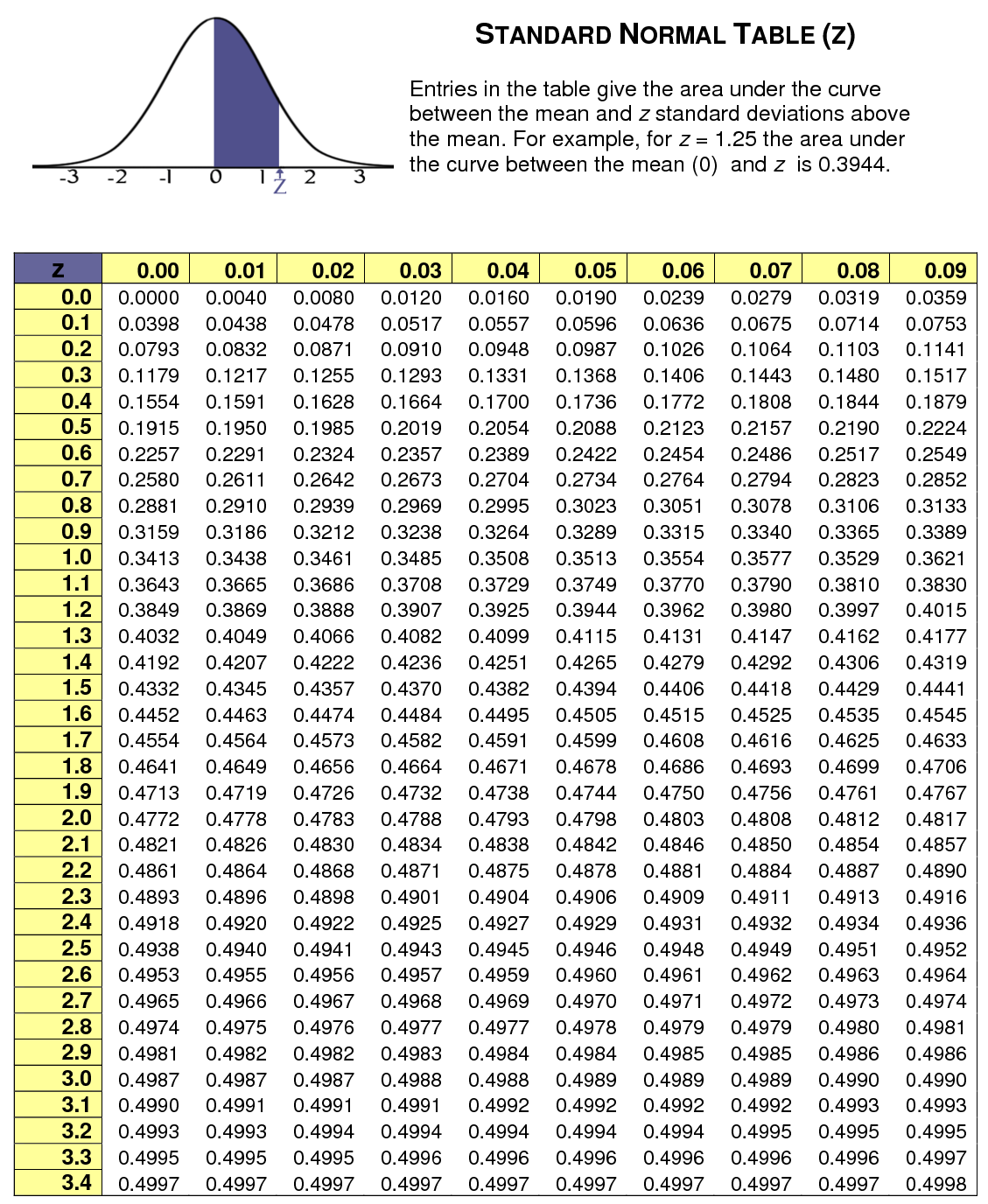
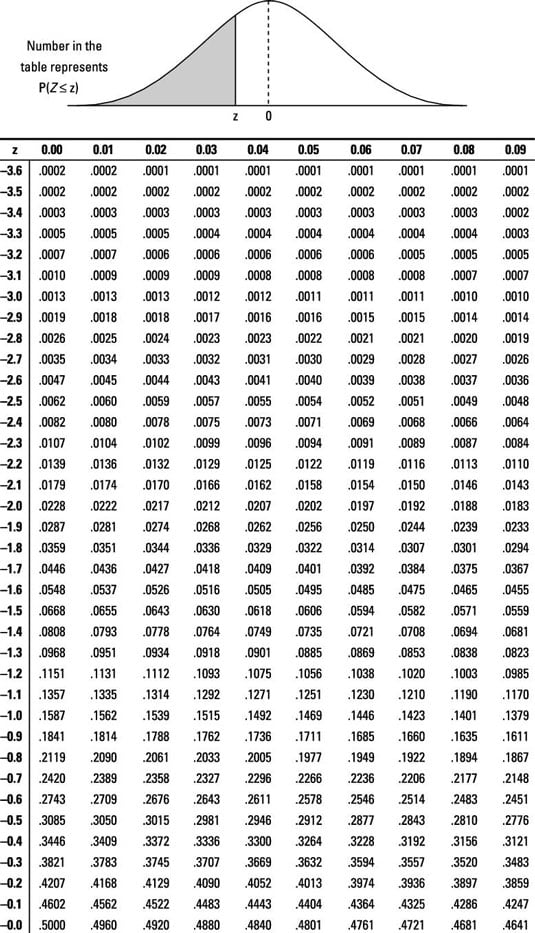
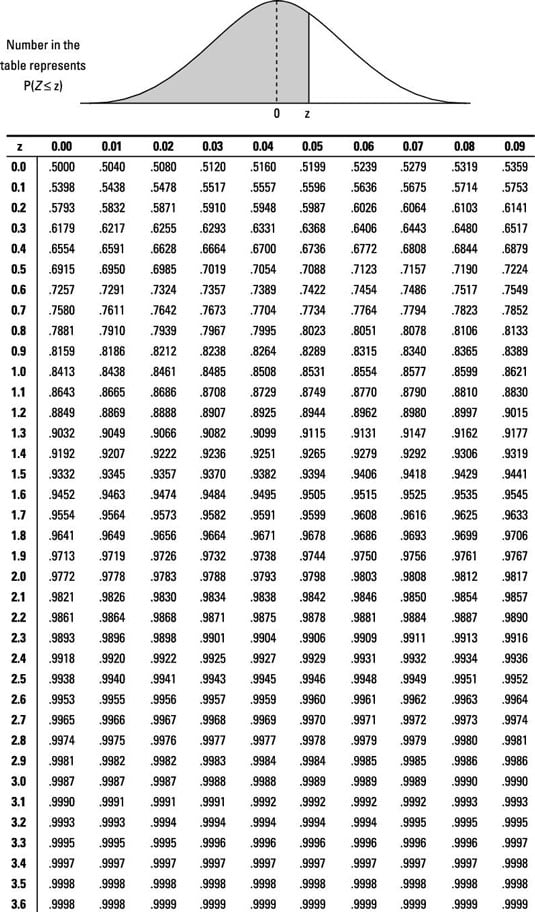
표준정규분포표는 위의 예시들처럼 두 가지 방법으로 나타나있다. 첫 번째의 경우에는 0에서 특정값 z까지의 확률 $P(0 <= Z <= z)$ 을 나타내는 것이고, 두 번째는 $-\infty$ 에서 특정값 z까지의 확률 $P(Z <= z)$ 을 나타내는 방법이다.

표준정규분포포(z-table) 에서 두 값들을 각각 찾아라. 예를 들어, z-값들이 각각 -0.46 과 +1.16 이라고 하면, 해당하는 값을 아래의 표에서 찾으면 된다. 우선은 소숫점 첫번째 자리까지의 값을 표 가장 왼쪽에서 찾고, 두 번째 자리의 값을 표의 윗쪽에서 찾은 다음 그 두 값이 만나는 곳이 0에서 그 값까지의 넓이이다. -0.46을 찾는 경우라면, 표준정규분포는 좌우대칭이기 때문에 0.46을 찾아도 되므로, 0.4가 있는 행과 0.06이 있는 열이 만나는 곳의 값인 0.1771이며, 이를 다시 나타내면 $P(0 <= X <= 0.46) = 0.1772$ 인 것이다. 동일한 방법으로 $P(0 <= X <= 1.16) = 0.3770$ 이다.

두 번째 표를 이용한다면 $ P(Z <= 1.16) = 0.8770, P(Z <= -0.46) = 0.3228 $ 이다.

2단계

첫 번째의 경우에는 이 두 값을 더하면 되고(0.3770 + 0.1772 = 0.5542, 두 번째 표를 이용한 경우라면 큰 값에서 작은 값을 빼면 된다(0.8770 - 0.3228 = 0.5542).

출처

• Area Between Two Z Values on Opposite Sides of Mean
• Video

• 2023 5
• 2022 1
• 2020 7
• 2019 24