Kyoyoung Chu

실험 기간을 좀 더 늘리면 안 돼요?

실험을 한 번 진행했는데 통계적으로 유의하지 못한 결과를 얻었습니다. 기간을 조금 더 두고 실험을 하자니 시간이 오래 걸릴 것 같은데 기존 결과를 그대로 포함해서 실험 기간을 늘려서 보면 안 되나요?

TL;DR

보는 것이야 자유이나, 실험 결과를 이용하여 의사결정을 내리고자 하는 용도라면 말리고 싶습니다. 그 이유는 아래에서 자세히 설명하겠지만, 이는 일종의 Peeking 이며 잘못된 의사결정을 내릴 가능성을 높이는 행위이기 때문입니다.

Peeking 이란 무엇이며, 왜 문제가 되는가

실험에서 Peeking 이란 충분한 표본이 모이지 않았을 때 그 결과를 확인하는 행위를 말합니다. 보다 자세한 내용은 What Is Peeking And How Do I Avoid It? 에서 확인할 수 있습니다.

Peeking 으로 발생할 수 있는 문제 중 하나로는 데이터 수집에서 발생한 편향 (bias) 이나 신기 효과 (novelty effect) 가 나타나는 실험 초기의 데이터만으로 성급하게 결론을 내릴 위험이 높다는 것입니다. 잘 설계된 실험이더라도 새로 소개된 기능을 많이 이용할 수 있으며, 이에 따라 초반에는 실험군의 지표가 대조군의 지표보다 높게/낮게 나올 수 있습니다. 그리고 아래와 같이 데이터를 보는 날에 따라 통계적 유의성이 달라질 수도 있습니다.

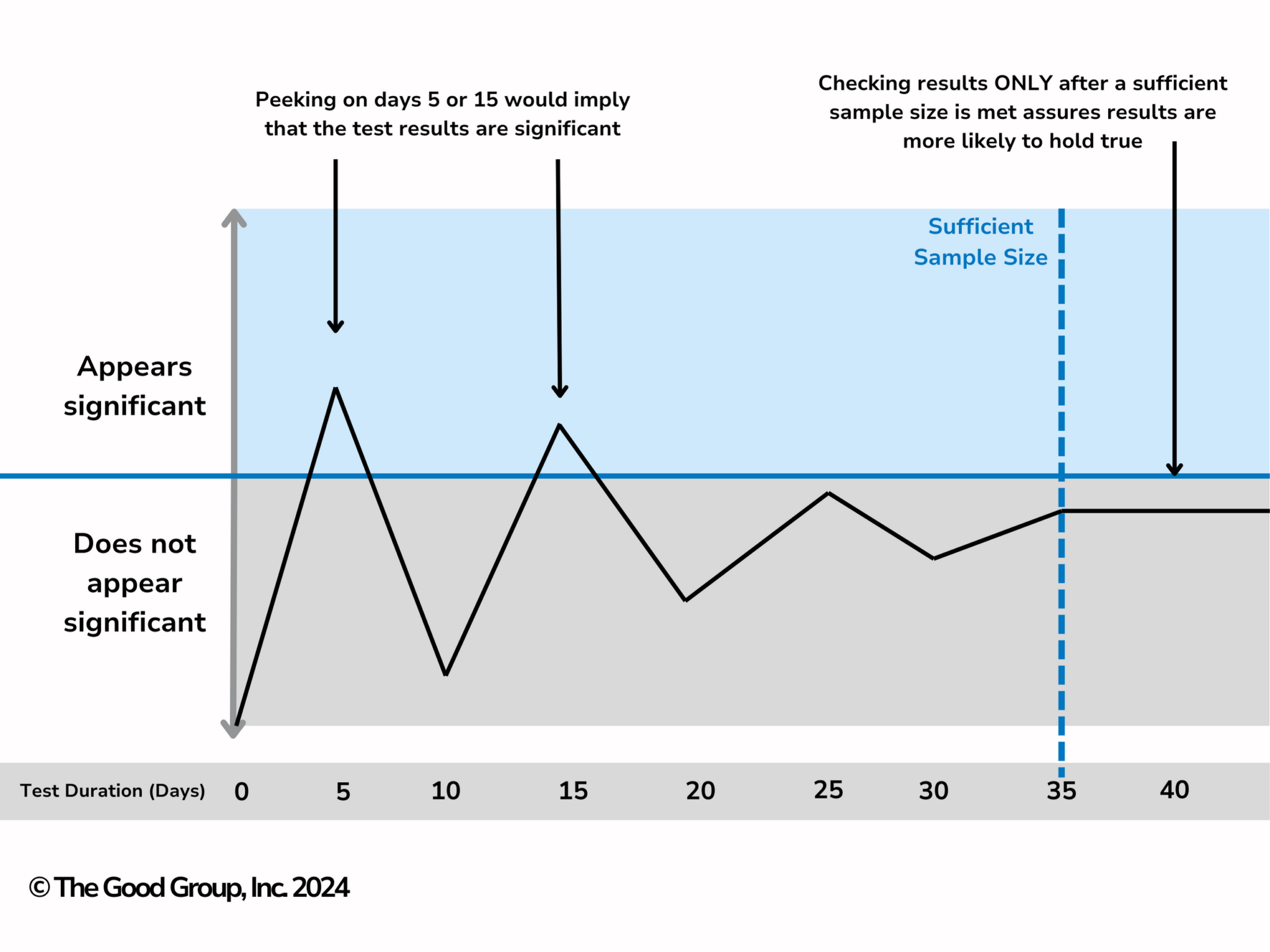
the-good-peeking-graph

그리고 다중비교문제 (multiple comparisons problem)

위에서 설명한 이유 외에도 다중비교문제 (multiple comparisons problem) 가 발생할 수 있습니다. 다중비교문제란 동시에 여러 가설 검정을 실시함으로 인해 제1종오류가 발생할 가능성이 커지는 것을 의미합니다. 일반적으로 유의수준을 0.05 로 설정한 상태에서 실험을 하는데, 이런 경우에도 두 집단 간에 차이가 없지만 있다고 잘못 판단할 확률이 5% 입니다. n번의 실험을 하는 경우 (각 실험이 독립적이라고 가정하더라도) 일련의 실험에서 모두 정확하게 판단할 확률은 $0.95^n$ 으로 4번만 Peeking 을 하더라도 해당 판단이 정확할 확률은 80% 수준으로 낮아집니다.

중간에 보고 싶으면 어떻게 하나요

서비스 트래픽이 적어서 충분한 표본을 모으는데 시간이 오래 걸릴 수 있습니다. 그런 경우 특히 Peeking 을 하고 싶은 욕구가 조금씩 생길텐데요. 이런 경우라면 몇 가지 사용해 볼 수 있는 방법이 있습니다.

첫 번째로, Peeking 을 하되, 의사결정은 내리지 않는 것입니다. Peeking 을 염두에 두고 실험을 설계하지 않은 경우에 할 수 있는 가장 쉬운 방법일 것입니다. 예를 들어, 실험 기간이 4주 정도 걸린다고 했을 때, 7일 단위로 경과를 살펴보더라도 중간에 통계적으로 유의한 차이를 확인하더라도 충분한 표본이 모일 때까지 의사결정을 보류하는 것입니다. 분명 누군가는 “아니 유의한 차이가 나왔는데 왜 배포를 하지 않느냐” 고 할 수 있기 때문에 사전에 이해관계자를 모아 놓고 왜 그래서는 안 되는지에 대해 설명하는 시간을 가져야할 수 있습니다.

두 번째는 유의수준을 교정하는 방법이 있습니다. 대표적인 방법으로는 본페로니 교정 (Bonferroni correction) 이 있습니다. 해당 방법은 각 실험의 유의수준을 실험 횟수로 나눠서 유의성을 검정하는 방법인데, 만약 10번의 Peeking 을 하는 경우 각 실험에서의 유의수준을 $0.05/10 = 0.005$ 로 설정하여 실험 결과를 해석하는 것입니다. 본페로니 교정은 가장 간단하고 단순한 형태이며 이에 맞는 실험 설계 방법이 필요할 수 있으며, 때에 따라서는 보다 복잡한 방법을 사용해야 하거나 사용할 수 있습니다.

세 번째는 조금 복잡한 방법인데, 축차 실험 (Sequential Testing) 의 형태로 실험을 설계하는 것입니다. 축차 실험은 표본의 크기를 사전에 정해놓지 않는다는 점에서 기존의 실험과 조금 다릅니다. 사전에 정해놓은 정지 규칙에 따라 실험의 중단을 결정하며, 경우에 따라서는 기간이나 표본의 크기를 정한 실험보다 빨리 끝낼 수도 있습니다. 축차 실험에서는 다양한 유의수준 소비 함수($\alpha$ spending function) 를 사용하는 게 가능하며, 이는 booking.com, Spotify, 그리고 Netflix 의 기술 블로그에서도 확인할 수 있습니다.

아래 그림은 Booking.com 의 글에서 발췌한 것인데, 표본의 크기 (X축) 가 커짐에 따라 추정치와 추정치의 신뢰구간이 작아지는 것을 확인할 수 있습니다. 즉, 표본의 크기가 작을 때는 클 때보다 넓은 신뢰구간을 가지며, 통계적으로 유의한 차이가 있다고 보기 위해서는 그 차이가 더 커야하는 것을 확인할 수 있습니다.

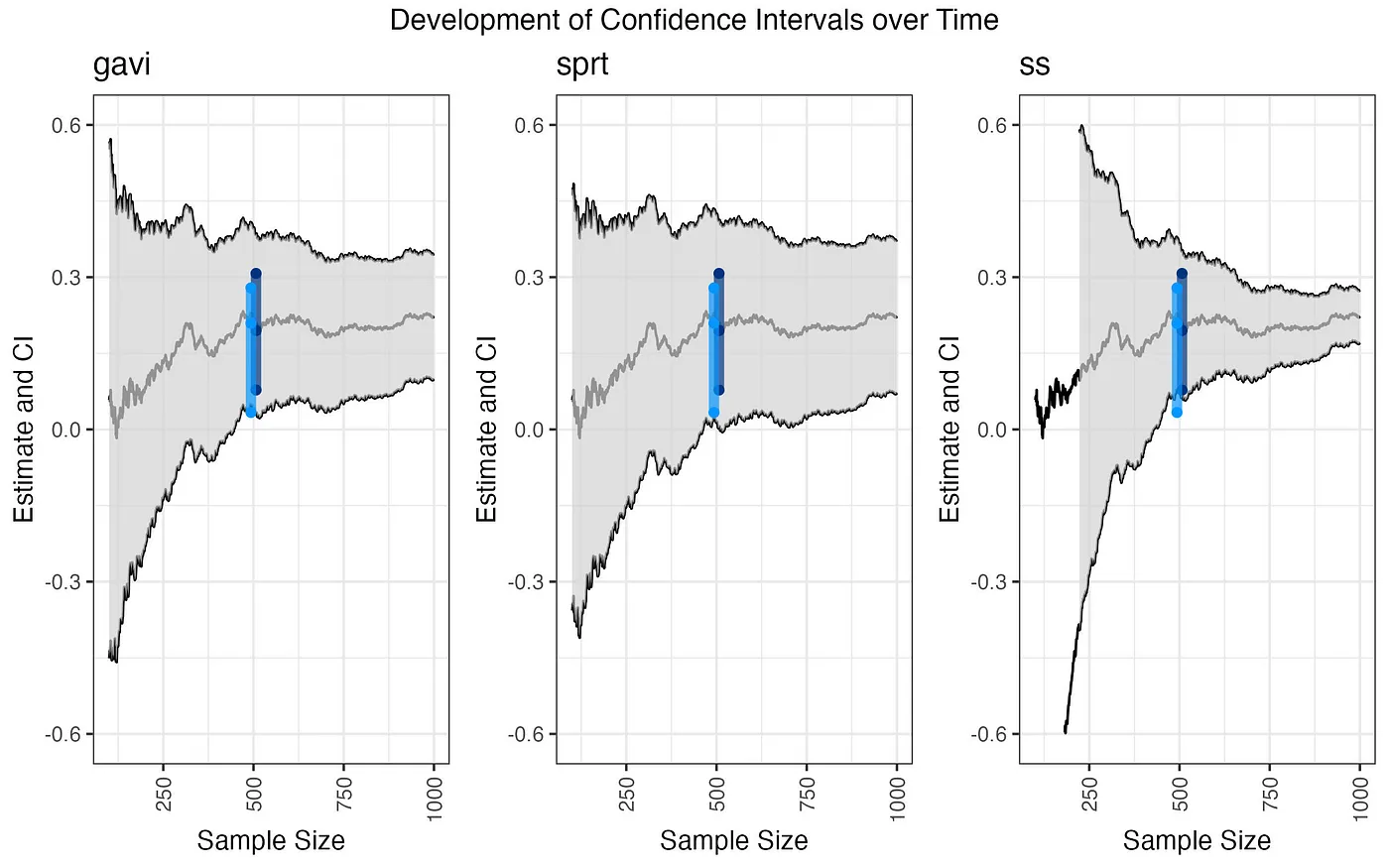
booking-dot-com-sequential-testing-comparison

References

2025

실험 기간을 좀 더 늘리면 안 돼요?

3 minute read

실험을 한 번 진행했는데 통계적으로 유의하지 못한 결과를 얻었습니다. 기간을 조금 더 두고 실험을 하자니 시간이 오래 걸릴 것 같은데 기존 결과를 그대로 포함해서 실험 기간을 늘려서 보면 안 되나요?

(번역) AI 가 우리에게 다가오고 있다

5 minute read

이 글은 AI가 데이터베이스에 직접 접근해 인간 전문가처럼 데이터를 분석하는 새로운 워크플로우를 소개합니다. 단순한 질의응답을 뛰어넘는 이러한 도약은 데이터 분석가의 역할이 근본적으로 재정의될 미래를 암시합니다.

(번역) 넷플릭스 게임 사용자의 모험

2 minute read

이 글은 넷플릭스 (Netflix) 에서의 분석 엔지니어링 (Analytics Engineering) 관련 업무의 범위를 공유하기 위한 여러 편의 글 중 두 번째 글이며, 최근에 열렸던 분석 엔지니어링 컨퍼런스에서 발표된 내용이기도 합니다. 더 많은 내용이 궁금하신가요? 첫 번째 ...

Back to top ↑

2023

영어랑 친해지는 방법

7 minute read

가장 좋은 방법은 당연히 영어 밖에 사용하지 못하는 환경에 강제로 처해지는 것이겠지만 그것이 어려우니…

Back to top ↑

2022

Back to top ↑

2020

사내 스터디에 대한 회고

2 minute read

회사 서비스의 추천 시스템을 개선하기 위해 팀 내에서 (아직까진 두 명이긴 하지만) 지난 두 달 동안 스터디를 진행했습니다. 얼마 전 두 번째 스터디가 끝났고 이에 대한 회고를 해보려고 합니다.

Back to top ↑

2019

GitHub Pages Jekyll Blog 에 MathJax 추가하기

3 minute read

이 글은 MathJax 를 GitHub Pages Jekyll blog 에 추가하는 방법을 다룬다. 이탤릭체로 된 부분은 본문에는 없고 제가 따라하면서 고치거나 추가한 부분이니 참고하세요.

GitHub 블로그에 Jupyter notebook 올리는 방법

4 minute read

여러분의 GitHub 블로그에 Jupyter notebook 을 바꿔서 올릴 수 있도록 도와줄 글입니다. 직접 바꾸는 방법은 1회성 글들을 위해서 추가했고, 변환 과정과 파일 이동, 그리고 여러분의 블로그에 올리는 것까지 한 번에 할 수 있는 자동화 bash 를 만드는 자세한 방법...

Back to top ↑