Kyoyoung Chu

듀오링고의 그로스 모델에 대한 오해

growth-model

들어가기에 앞서

원문: What everyone gets wrong about the Duolingo growth model - Justin Goff

관련 글

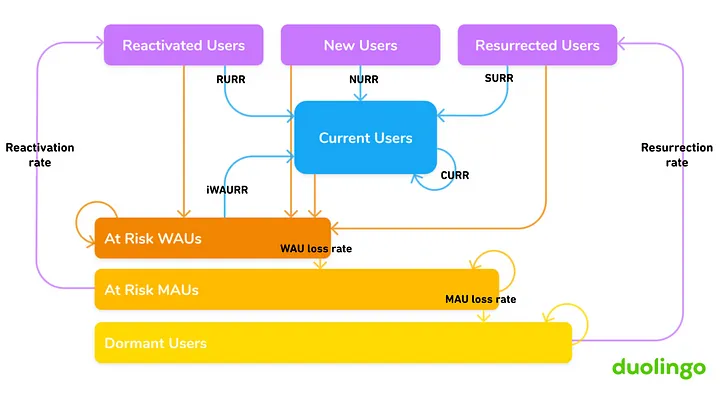
듀오링고의 그로스 모델에 대한 이야기는 Erin Gustafson 박사와 듀오링고의 CPO 를 역임했던 Jorge Mazal 이 말한 것처럼 아주 재미있습니다.

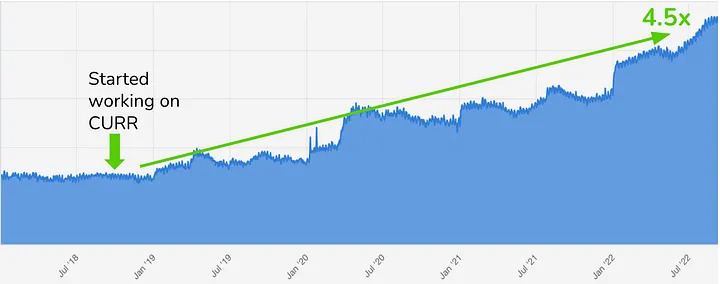
2018년, 듀오링고의 성장세는 한풀 꺾이기 시작했고, DAU 를 직접적으로 올리려고 노력했으나, 결과도 안 좋아지기 시작했습니다.

직관과 이전 회사에서의 경험, 그리고 정교한 모델링의 조합을 통해 듀오링고는 새로운 북극성 지표 (현재 사용자 유지율; CURR) 에 도달했고, 이 때 시작된 DAU 의 성장 기세는 현재까지도 멈추지 않고 있습니다.

the-kind-of-dau-graph-pms-dream-of

자, 저는 그 당시 그로스 모델에 직접적으로 관련이 있는 팀에 속하지는 않았지만, 내부에서 들은 이야기는 여전히 대단했습니다.

문제는 이 이야기의 중요한 몇몇 부분이 전달되는 과정에서 생략되었다는 것입니다. 그 결과, 제품 관리자 (Product Manager) 들은 듀오링고의 그로스 모델에서 종종 이상한 점을 배우고자 했습니다. 이 경우 잘 해봐야 불필요한 방해 요소가 될 뿐이며, 최악의 경우 제품의 성장을 해칠 수도 있습니다.

문제 1: 여러분은 듀오링고가 아닙니다

듀오링고의 그로스 모델에 대한 이야기는 너무나도 매혹적이어서, 이 결과가 한 특정 회사의 어떤 특정 시점에서 벌어진 일이라는 사실을 쉽게 잊어버리곤 합니다.

Erin 과 Jorge 는 글에서 이 내용을 매우 강조했습니다. 이 모델은 2018년 듀오링고가 가지고 있던 과거 데이터를 학습했으며, 시뮬레이션은 2018년의 듀오링고에게 맞춰진 입력값을 이용했습니다. 다시 말하면,

CURR 에 집중하고자 한 결정은 2018년의 듀오링고에 한정된다는 것입니다.

그 당시 듀오링고는 현재 사용자 그룹에 엄청나게 많은 사용자들이 있었고, 이는 절대적인 수치 뿐만 아니라, 다른 그룹과 비교를 해봐도 마찬가지였습니다. Jorge 가 본인의 글에서 밝혔듯이, 다양한 시나리오 중에서 CURR 을 선택할 가능성이 높았던 수리적인 이유가 있었습니다만 (CURR 은 복리적 효과가 있었습니다), 모든 시나리오에서 CURR 을 향하는 것만은 아니었습니다.

예를 들어, 현재 사용자는 적으나, 매일 들어 오는 신규 사용자가 아주 많은 상황이라면, 여러분은 CURR 하나에만 집중하는 것보다, NURR 과 CURR 사이에 적절한 균형을 이루는 편이 훨씬 더 빠르게 성장할 수 있을 것입니다. 다시 말하자면, 현재 사용자 수가 상대적으로 적은 편이라면 CURR 에만 집중해서는 성장에 오랜 시간이 걸릴 겁니다.

문제 2: 여러분은 듀오링고가 아닙니다 (아직은)

듀오링고의 그로스 모델에 대해 사람들이 가지는 또 다른 큰 오해는, 듀오링고는 2018년 이전까지는 그로스 모델이 없었다는 것입니다.

2018년에 듀오링고는 설립된 지 7년 정도 된 회사였고, 7억 달러의 가치를 인정 받아서 시리즈 E 까지 유치했으며, 유니콘이 되기까지 불과 몇 달 밖에 안 남았다는 사실입니다 (2019년 12월 시리즈 F 를 유치하면서 15억 달러의 가치를 인정 받았습니다).

듀오링고는 그로스 모델 이전에도 시장에 맞는 제품을 가진 상태였고, 리텐션은 높았으며, 자연적으로도 (organic) 급격하게 성장하는 중이었습니다.

중요한 것은, 듀오링고의 그로스 모델은 저렴하지 않으며, 어느 정도 수준에 이르지 못한다면 여러분이 모르는 것에 대해 별로 알려줄 게 없다는 사실입니다 (더 많은 사용자를 유치하고, 사용자들이 더 자주 방문하게 만들어야만 합니다). 초반이라면, 여러분은 듀오링고 스타일의 모델을 만드는데 많은 시간을 쏟게 될 것이며, 이는 기본적인 지표들에 집중하고, 간단한 경험 법칙을 적용하는 것보다 빠른 성장을 돕지도 못할 것입니다.

그렇다면 중요한 것은 무엇인가요?

결국, 듀오링고 그로스 모델에서 배울 점은 모두가 CURR 에 집중해야 한다거나, 듀오링고 스타일의 그로스 모델을 만들어야 한다는 것이 아닙니다.

배워야 하는 것은 제대로된 북극성 지표를 선택하는 것은 성장에 필수적이다 라는 것입니다.

2018년 듀오링고는 기존의 지표들이 점점 덜 유용해지고 있다는 신호를 감지했습니다. 통계적 모델링을 통해 몇 가지 유망한 북극성 지표를 찾아내기도 했고, 제품 안에서 실제 사용자들에게 실험을 하면서 유효성을 증명하기도 했습니다. (사람들이 간과하는 부분이기도 한데, 저희도 모델에서 검토해봐야 한다고 한 다른 지표들만큼 쉽게 CURR 을 변화시킬 수 있다고 확신하지 못했습니다).

초반에는 활성 사용자와 같은 높은 수준에서의 북극성 지표가 의미있을 것입니다. 여러분은 쉽게 얻을 수 있는 것들을 많이 가지고 있으며, 당길 수 있는 수많은 레버들이 있을 것입니다. 그러니 CURR 과 같은 하나의 인풋 지표 (input metric) 에 매몰 되어 시간을 허비하지 않길 바랍니다. 성장은 때로 뻔한 것을 최대한 빠르게 실행함으로써 얻을 수도 있습니다.

그러고 나서, 여러분이 2018년의 듀오링고처럼 되는 행운을 얻게 된다면, 듀오링고의 그로스 모델을 써먹어 보시기 바랍니다.

2025

Back to top ↑

2023

영어랑 친해지는 방법

7 minute read

가장 좋은 방법은 당연히 영어 밖에 사용하지 못하는 환경에 강제로 처해지는 것이겠지만 그것이 어려우니…

Back to top ↑

2022

Back to top ↑

2020

사내 스터디에 대한 회고

2 minute read

회사 서비스의 추천 시스템을 개선하기 위해 팀 내에서 (아직까진 두 명이긴 하지만) 지난 두 달 동안 스터디를 진행했습니다. 얼마 전 두 번째 스터디가 끝났고 이에 대한 회고를 해보려고 합니다.

Back to top ↑

2019

GitHub Pages Jekyll Blog 에 MathJax 추가하기

3 minute read

이 글은 MathJax 를 GitHub Pages Jekyll blog 에 추가하는 방법을 다룬다. 이탤릭체로 된 부분은 본문에는 없고 제가 따라하면서 고치거나 추가한 부분이니 참고하세요.

GitHub 블로그에 Jupyter notebook 올리는 방법

4 minute read

여러분의 GitHub 블로그에 Jupyter notebook 을 바꿔서 올릴 수 있도록 도와줄 글입니다. 직접 바꾸는 방법은 1회성 글들을 위해서 추가했고, 변환 과정과 파일 이동, 그리고 여러분의 블로그에 올리는 것까지 한 번에 할 수 있는 자동화 bash 를 만드는 자세한 방법...

Back to top ↑